【简明教程】复习算法
这篇文章介绍了拾忆笔记在复习算法上的设计思想
复习材料
复习材料可以分为两类,第一类是以“单词”、“知识点”为代表的“小体量”复习材料,由于所含的知识点单一,因此复习一次所需的时间很短,例如下面的问答题:
问:世界上第二高的山峰?
答:乔戈里峰
第二类是以“数学试题”、“笔记”为代表的“大体量”复习材料,由于包含了多个知识点,复习一次所花费的时间较长,复习成本较高。
| 复习材料 | 常见例子 | 特点 |
|---|---|---|
| 小体量材料 | 单词、基本知识点 | 知识点单一、复习成本低 |
| 大体量材料 | 试题、笔记 | 由多个知识点组成、复习成本高 |
小体量材料复习算法背后的逻辑
小体量材料的遗忘规律遵循指数形式,即艾宾浩斯遗忘曲线;一段时间后的记忆保留百分比可用如下公式描述:
计算记忆保留率的前提是测定记忆材料难度、记忆强度,因此记忆辅助软件通常会引入 “评分面板”,依靠用户的显式评分不断修相关参数。通常,相关参数的获得需要多次评分,由于小体量材料复习耗时较少,且相较于遗忘后的重新记忆成本,在时间支出上存在收益,因此高频(一天内复习多次)、多次(复习周期内>10次)的复习策略较为常见。
大体量材料不应追求精确的复习算法
1.大体量材料复习成本过高
复习算法若想较为准确地刻画复习材料的遗忘规律需要用户提供多次评分,评分次数是预测准确度的保证,但是大体量材料的复习成本较高,在复习材料数量较多的情况下,复习频繁过高会导致效率问题,因为复习行一方面会带来收益,一方面也会付出时间成本。例如不进行复习可能会导致随学随忘、收获寥寥,但拘泥于对旧知识的复习也会挤占学习新知识的时间。
2.大体量材料遗忘规律不同于小体量记忆材料
单一知识点符合上文介绍的指数遗忘规律,大体量材料由多个知识点构成,每个知识点有其各自的难度,因而遵循各自的指数遗忘形式,大体量材料整体的遗忘形式是则各组成部分的叠加,叠加后一般反应为线性形式,即意味着大体量材料的遗忘速度是更缓慢的:
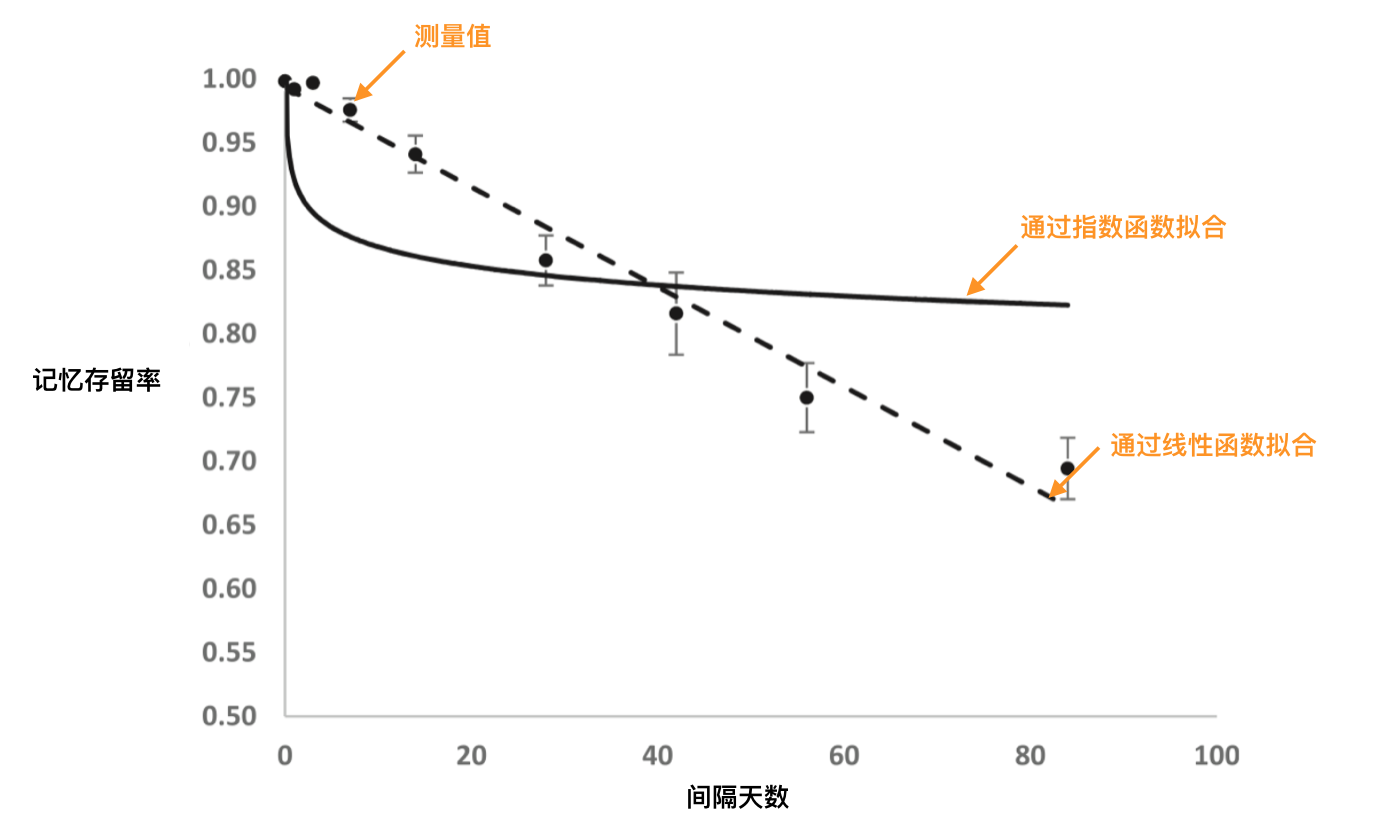
这一结果可以从两方面直观地解释:
1.大体量材料通常是具有意义的 指数遗忘曲线是在单词这类无意义、难以解释的材料上测得的,而大体量材料通常能够被理解与解释,因而遗忘速度较慢。
2.大体量材料各组分之间存在“连带效应” 大体量复习材料是由多个知识点构成的集合体,且每个知识点之间存在联系,因此未被遗忘的部分会起到“提示作用”。
由于大体量材料与小体量材料的遗忘规律不同,即导致适用于小体量材料的复习算法、复习策略并不适用于大体量材料。
剂量与毒性
不乏这样的疑问:“我用小体量记忆算法(Anki)来记忆大体量材料(试题)感觉效果也很好呀”?
从记忆效果上来讲必定是更好的,因为小体量记忆算法的复习周期更紧密,即复习次数更多。题目自然是做的次数越多,理解越到位,效果越好。
真正的问题在于“复习压力”,如果仅仅记忆几十道题目,一天的复习量不会太多,小体量记忆算法同样可行,但是,如果目标是500道题目呢?假设复习一个单词,平均用时5秒钟,复习一道题目,平均用时5分钟,题目的复习成本是单词的60倍,则500道题目的复习成本相当于30000个单词,假设一天复习10道题目,则一天在复习上的投入将会花费50分钟。
因此,抛弃小体量记忆算法是从“全局”角度出发的,为了整体效率而在单个题目的记忆效果上做出取舍。大体量材料复习过程的“高成本”迫使复习笔记数量应有限度、复习行为应低频,低频也导致记忆目标发生变化,记忆目标从 “不能遗忘” 到 “允许遗忘” ,允许“先部分忘记”等用到时再 “拾起来”,允许记忆材料的熟悉程度降低到 “遗忘线” 之下,进而,每次复习从关乎“复习效果”到关乎“复习过程”。
更详细的讨论见《复习原理》
复习算法
复习算法可划归为三类:
1.自主安排:由用户自主决定复习间隔,因此并不属于“智能”的范畴,依靠的是使用者的经验,特点是灵活性高,对于并不追求算法精确度的大体量复习材料而言极为适用。
2.经验公式:指以SM2、Anki为代表的复习算法,计算结果基于经验公式,特点是在软件代码实现上极为简单,因此较为常见。
3.机器学习技术:即所谓的“AI"与"智能",在效果上已全面超越经验公式,主要涵盖循环神经网络、[随机过程](Enhancing human learning via spaced repetition optimization)、强化学习、排队论。
| 复习算法 | 算法性质 | 适用对象 |
|---|---|---|
| 预设间隔 | 自主安排 | 大体量材料 |
| 神经网络 | 机器学习 | 大体量材料 |
| Anki | 经验公式 | 小体量材料 |
| SM2 | 经验公式 | 小体量材料 |
拾忆笔记并非为小体量材料复习而设计,出于实现难度考虑在小体量算法的实现上选用了Anki、SM2,两者都基于”经验公式“(从历史角度上来讲,Anki算法源于SM2算法),在效果上难以企及各类基于机器学习技术的算法,因此,如果你的目标是背单词,从算法角度上来讲,墨墨、百词斩之类的专业产品会是更明智的选择。
预设间隔
按照固定的间隔进行复习,如间隔1、5、15、30即代表要复习四次,间隔依次为1天、5天、15天、30天
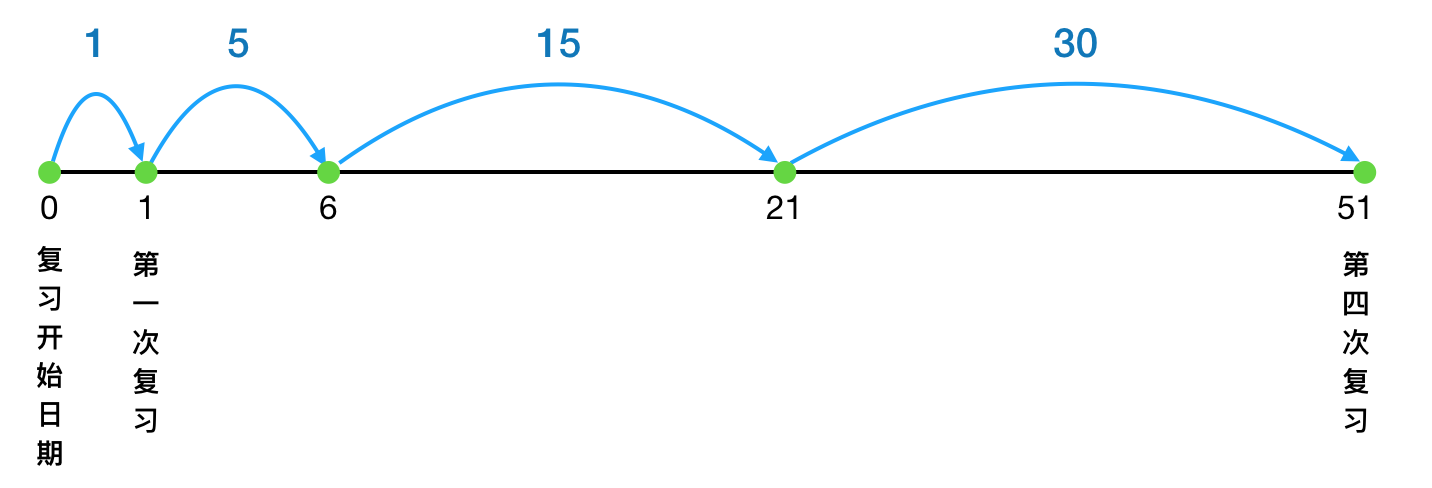
复习间隔在选取上是具有经验性的,一般的意见是:大跨度,下次复习间隔是上次的2~3倍。
以复习间隔 1、5、15、30、60 为例:
总计复习次数5次,累计时间跨度:1+5+15+30+60=111天
| 间隔 | |
|---|---|
| 1 | 今天学习,明天复习 |
| 1->5 | 五倍关系 |
| 5->15 | 三倍关系 |
| 15->30 | 两倍关系 |
| 30->60 | 两倍关系 |
1->5 倍数定的较高,源于通过5天的设置将复习间隔快速“拉”起来,并且间隔5天并不会毫无印象
神经网络
基于Duolingo 于2016年提出的HLR复习算法,通过在算法设计中引入“复习目标”,从而使得算法适用于大体量记忆材料。
SM2
基于SuperMemo于1995年提出的SM2复习算法
Anki
基于Anki 复习算法,并在原算法基础上移除了复习间隔“小于一天”的复习逻辑
复习参数设置
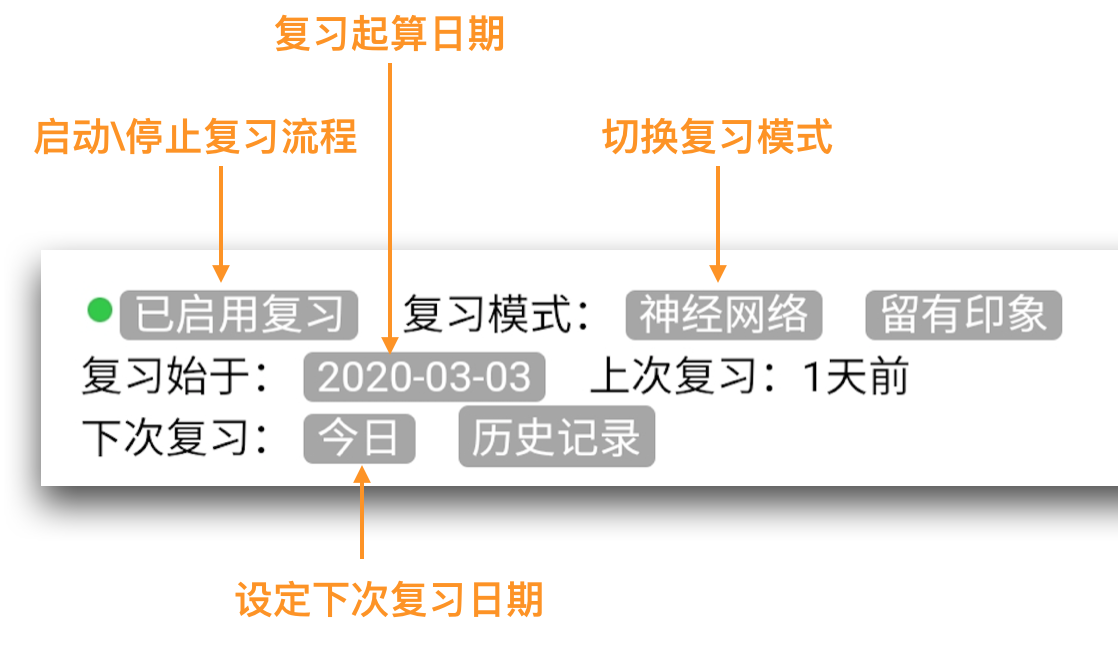
下次复习日期
考虑到现实情况的复杂性,算法不应作为绝对真理。
在拾忆笔记中可以自由设定“下次复习日期”,对于“评分类”复习算法(Anki、SM2、神经网络),若对评分安排存在异议,可评分后手动修改“下次复习日期”。
直接修改“下次复习日期”与评分后再修改的区别在于评分会产生一条复习记录,该记录可用于更好地刻画材料难度,以提高算法预测准确度。
常见问题
如何应对复习材料的“累积”问题?
复习如同杂技演员接抛球,每天都有新的复习材料加入,如同向空中抛出越来越多的球,复习压力也越来越大。

策略1:由“不忘”到“拾忆”
采用较大的复习间隔,降低单个材料的记忆效果,复习目标从“全程保持不忘”转移到考前“快速拾起”。
策略2:整理总结
读书是先读到厚,再读薄的过程,这源于认识是一个由“复杂到简单”的过程,一步步螺旋式深入,到最后归纳出简单的本质;整理一下所学过的内容,常会发现一些知识可以被整合,因此也就减小了复习任务量。
策略3:更替
即“以新代旧”,学习应是个“有进有出”的过程,需要有“源头活水”来,不妨停止一些旧知识点的复习,因为日后还会见到同一知识点的新应用。
策略4:平衡策略
通过观察可以发现一种普遍现象——有的时候复习任务很多,但有的时候复习任务却很少。因此可引入“平衡”策略。相关功能正在研发中,敬请期待拾忆笔记1.0.70版~
为何评分不同但拾忆笔记给出的时间安排却是相同的?
因为算法中存在“修正策略”,例如:
1.拾忆笔记中复习间隔的最小值为1天,因此小于1天的复习间隔会被提升至1天。
2.为防止复习间隔过于密集\稀疏,Anki、SM2复习算法对于复习材料的难度值有限定,难度值存在下限值1.3(SM2算法亦存在上限值2.5),若不同评分所得出材料难度值小于1.3 则均会提升至1.3计算,导致时间安排一致。